Funciones cuadráticas.
Las gráficas de estas funciones
corresponden a parábolas verticales (eje de simetría
paralelo al eje de las ordenadas), con la particularidad de que cuando a>0,
el vértice de la parábola se encuentra en la parte
inferior de la misma, siendo un mínimo (es decir, la parábola se abre
"hacia arriba"), y cuando a<0 el vértice se encuentra
en la parte superior, siendo un máximo (es decir, la parábola se abre
"hacia abajo").
un ejemplo de función
cuadrática seria:
El vértice del ejercicio 1 es el
vértice máximo
ecuación cuadrática
ecuaciones cuadráticas de la forma ax2=0
En este caso la respuesta siempre será 0.
ecuaciones cuadráticas de la forma ax2+bx=0
Para resolver este tipo de ecuaciones basta sacar factor común a la x e igualar los 2 factores a cero.
Una ecuación cuadrática de forma ax2 +
bx + c.
2. Fórmula Cuadrática
( x
+ ) (x - ) = 0 hay que buscar 2 números que multiplicados me den – 8 y sumados o restados me den +2.
x = 0 –
4 x = 0 + 2
x =
-4 x =
2
Estas son las dos soluciones.
Fórmula Cuadrática:
x = -2 ± 6
2
2
2
2
2
Ejemplos:
Posiciones relativas entre una recta y una parábola
Para determinar las posiciones relativas entre una recta y una
parábola, se remplaza la ecuación de la recta en la de la parábola.
Ejemplo:
Mas Ejercicios Resueltos.
SISTEMAS CUADRÁTICOS.
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten dos o más incógnitas. Las soluciones de un sistema de ecuaciones son todos los valores que son válidos para todas las ecuaciones, o los puntos donde las gráficas de las ecuaciones se intersectan.
Podemos resolver un sistema de ecuaciones lineales graficando, por sustitución y por combinación lineal. Los sistemas de funciones no lineales, como ecuaciones cuadráticas o exponenciales, pueden ser manejados con las mismas técnicas.
CUANDO SON SOLUCIONES O NO
Empecemos por hablar sobre dos ecuaciones lineales. La solución de este tipo de sistema es el punto de intersección entre las dos rectas, o el lugar donde las dos ecuaciones tienen los mismos valores de x y de y. Puede haber más de una solución, no solución, o un número infinito de soluciones de un sistema de dos ecuaciones lineales:
Ejemplo:
INECUACIONES CUADRÁTICAS
Una inecuación cuadrática es una inecuación de la forma:
a x 2 + b x + c < 0
TAMBIÉN:
Las desigualdades son expresiones de la forma A<B, donde
A y B pueden ser expresiones numéricas ó algebraicas y el símbolo
"<(menor que)" podría ser
>(mayor que) ó ≤(menor ó igual
que)" ó ≥(mayor ó igual que). A la
expresión que hay a la izquierda le llamaremos primer miembro y a la que hay a
la derecha, segundo miembro.
Regla de la suma: Si sumamos (o restamos) una misma cantidad
a los dos miembros de una desigualdad, obtenemos otra desigualdad equivalente
del mismo sentido. O sea, A<B Û A+C<B+C para cualquier cantidad C.
Una inecuación es una desigualdad entre expresiones
algebraicas. A las letras de dichas expresiones algebraicas les llamaremos
incógnitas, y dependiendo de cuantas haya, diremos que se trata de una
inecuación con una, dos, tres,...incógnitas.
En el video se muestran de cuantos metodos se podrá resolver
Ejercicios.
a ) d )
d )  b )
b ) e )
e )  c )
c ) f )
f ) Inecuaciones con 2 Incógnitas
Inecuaciones con 2 Incógnitas
Vamos a estudiar ahora inecuaciones con dos incógnitas (x e y), en este caso al graficar la solución, en lugar de hacerlo en un sistema de ejes cartesianos, es decir se graficará en el plano.
Una inecuación con dos incógnitas, determina una región del plano, (de hecho inclusive una inecuación con una incógnita también puede determinar una región del plano, como veremos más adelante).
EJEMPLO
Ejercicios.
a) 3x+4y > 12;
b) 2x+3y £ 6;
c) x + 2y + 4 ³ 0
Sistema de Ecuaciones cuadráticas.
EJERCICIO RESUELTO
12x2 − 3x = 0
4x2 − x = 0
x · (4x −1) = 0
x = 0
4x − 1 = 0 x = 1/4
4
 VIDEO:
VIDEO:
Ecuaciones con
valor absoluto.
El valor absoluto describe la
magnitud de un número o
la distancia entre puntos, pero ignora la información
del
signo del número o la dirección de una distancia.
Un valor absoluto
positivo puede representar ya sea un valor original positivo o negativo.
Cuando
simplificamos o resolvemos ecuaciones que
incluyen expresiones con valores
absolutos, debemos
considerar ambas posibilidades.
El vértice del ejercicio 1 es el
vértice máximo
ecuación cuadrática
ecuaciones cuadráticas de la forma ax2=0
En este caso la respuesta siempre será 0.
ecuaciones cuadráticas de la forma ax2+bx=0
Para resolver este tipo de ecuaciones basta sacar factor común a la x e igualar los 2 factores a cero.
Una ecuación cuadrática de forma ax2 +
bx + c.
Ejemplo:
9x2 + 6x +
10 a = 9, b = 6, c = 10
3x2 -
9x
a = 3, b = -9, c = 0
-6x 2 +
10
a = -6, b = 0, c = 10
Hay tres formas de hallar las raíces ( el o los valores de la variable) de
las ecuaciones cuadráticas:
1. Factorización Simple
2. Fórmula Cuadrática
2. Fórmula Cuadrática
Factorización Simple:
La factorización simple consiste en convertir la ecuación cuadrática
en un producto de binomios. Luego, se busca el valor de x de cada binomio.
Ejemplo: Realizar la factorización simple de la ecuación
x2 + 2x – 8 =
0 a = 1
b = 2 c = - 8
(x + ) (x –
) =
0
[x ·x = x2]
( x
+ ) (x - ) = 0 hay que buscar 2 números que multiplicados me den – 8 y sumados o restados me den +2.
|
(x + 4 ) (x – 2) =
0
4 y –2 4 + -2 = 2
4 · -2 = -8
x + 4 = 0 x – 2 = 0
x + 4 = 0 x – 2 = 0
x = 0 – 4 x = 0 + 2
x = -4 x = 2 Estas son las dos soluciones.
x = 0 – 4 x = 0 + 2
x = -4 x = 2 Estas son las dos soluciones.
Fórmula Cuadrática:
Este método es muy simple: hay que sustituir los valores de a, b y c
de la ecuación cuadrática a la siguiente fórmula:
Ejemplo:
X2 + 2x – 8 = 0 a = 1, b = 2,
c = -8
x = -2 ± 6
2
2
X = -2 + 6 x = -2 - 6
2 2
2 2
x = 4
x = -8
2 2
2 2
x = 2 x = - 4
Ejemplos:
https://www.youtube.com/watch?v=WfSwWQHg2tQEjemplos:
Posiciones relativas entre una recta y una parábola
Para determinar las posiciones relativas entre una recta y una parábola, se remplaza la ecuación de la recta en la de la parábola.
Ejemplo:
Para determinar las posiciones relativas entre una recta y una parábola, se remplaza la ecuación de la recta en la de la parábola.
Ejemplo:
Mas Ejercicios Resueltos.
SISTEMAS CUADRÁTICOS.
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten dos o más incógnitas. Las soluciones de un sistema de ecuaciones son todos los valores que son válidos para todas las ecuaciones, o los puntos donde las gráficas de las ecuaciones se intersectan.
Podemos resolver un sistema de ecuaciones lineales graficando, por sustitución y por combinación lineal. Los sistemas de funciones no lineales, como ecuaciones cuadráticas o exponenciales, pueden ser manejados con las mismas técnicas.
CUANDO SON SOLUCIONES O NO
Empecemos por hablar sobre dos ecuaciones lineales. La solución de este tipo de sistema es el punto de intersección entre las dos rectas, o el lugar donde las dos ecuaciones tienen los mismos valores de x y de y. Puede haber más de una solución, no solución, o un número infinito de soluciones de un sistema de dos ecuaciones lineales:
Ejemplo:
INECUACIONES CUADRÁTICAS
Una inecuación cuadrática es una inecuación de la forma:
o cualquier expresión de la forma anterior que, en lugar del símbolo < incluya cualquier otro símbolo de desigualdad: > , ≤ o ≥
.
TAMBIÉN:
Las desigualdades son expresiones de la forma A<B, donde
A y B pueden ser expresiones numéricas ó algebraicas y el símbolo
"<(menor que)" podría ser
>(mayor que) ó ≤(menor ó igual
que)" ó ≥(mayor ó igual que). A la
expresión que hay a la izquierda le llamaremos primer miembro y a la que hay a
la derecha, segundo miembro.
Regla de la suma: Si sumamos (o restamos) una misma cantidad
a los dos miembros de una desigualdad, obtenemos otra desigualdad equivalente
del mismo sentido. O sea, A<B Û A+C<B+C para cualquier cantidad C.
Regla del producto: Si multiplicamos (o dividimos) los dos miembros de una desigualdad por una
misma cantidad (distinta de cero) , obtenemos otra desigualdad equivalente, del
mismo sentido si C>0 y de sentido contrario si C<0. O sea, A<B
Û (A·C<B·C si C es una cantidad positiva ó A·C>B·C si C es una
cantidad negativa).
Una inecuación es una desigualdad entre expresiones
algebraicas. A las letras de dichas expresiones algebraicas les llamaremos
incógnitas, y dependiendo de cuantas haya, diremos que se trata de una
inecuación con una, dos, tres,...incógnitas.
En el video se muestran de cuantos metodos se podrá resolver
Ejercicios.
a ) d )
d ) 
b ) e )
e ) 
c ) f )
f )
Inecuaciones con 2 Incógnitas
Vamos a estudiar ahora inecuaciones con dos incógnitas (x e y), en este caso al graficar la solución, en lugar de hacerlo en un sistema de ejes cartesianos, es decir se graficará en el plano.
Una inecuación con dos incógnitas, determina una región del plano, (de hecho inclusive una inecuación con una incógnita también puede determinar una región del plano, como veremos más adelante).
Ejercicios.
c) x + 2y + 4 ³ 0
Sistema de Ecuaciones cuadráticas.
EJERCICIO RESUELTO
12x2 − 3x = 0
4x2 − x = 0
x · (4x −1) = 0
x = 0
4x − 1 = 0 x = 1/4
4


VIDEO:
Ejercicios.
Ecuaciones con
valor absoluto.
El valor absoluto describe la
magnitud de un número o
la distancia entre puntos, pero ignora la información
del
signo del número o la dirección de una distancia.
Un valor absoluto
positivo puede representar ya sea un valor original positivo o negativo.
Cuando
simplificamos o resolvemos ecuaciones que
incluyen expresiones con valores
absolutos, debemos
considerar ambas posibilidades.
1) |x| = 4
2) |3x| = 5
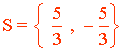
Inecuciones con valor absoluto.
Una inecuación con valor absoluto es un tipo de inecuación que contiene un valor absoluto. Un valor absoluto mide la distancia donde se encuentra un número hasta 0, por ejemplo, |x| mide la distancia de x hasta 0. Las inecuaciones con valor absoluto son útiles en simetrías, límites simétricos o condiciones de borde. Entiende y resuelve este tipo de inecuaciones con algunos pasos simples, ya sea mediante evaluación o transformación.
|x| ≤ a se expresa como:
- a ≤ x ≤ a

Inecuciones con valor absoluto.
Una inecuación con valor absoluto es un tipo de inecuación que contiene un valor absoluto. Un valor absoluto mide la distancia donde se encuentra un número hasta 0, por ejemplo, |x| mide la distancia de x hasta 0. Las inecuaciones con valor absoluto son útiles en simetrías, límites simétricos o condiciones de borde. Entiende y resuelve este tipo de inecuaciones con algunos pasos simples, ya sea mediante evaluación o transformación.
|x| ≤ a se expresa como:
- a ≤ x ≤ a








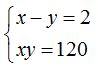
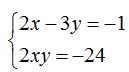

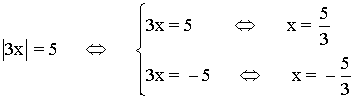
No hay comentarios.:
Publicar un comentario